99. 岛屿数量
题目描述
题目描述:
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述:
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
3
提示信息
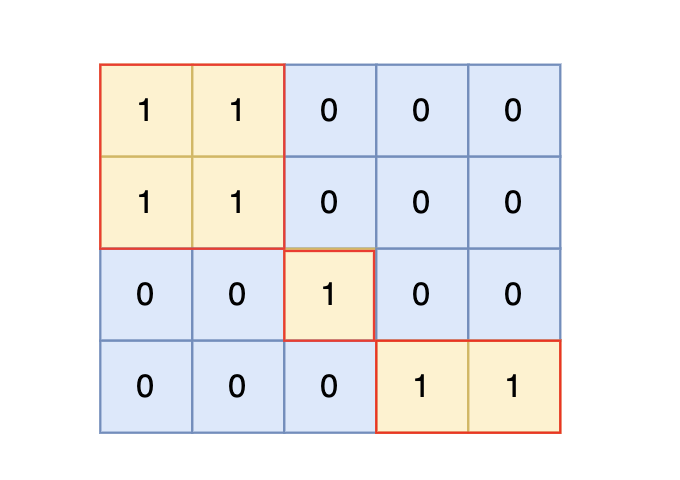
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
数据范围:
- 1 <= N, M <= 50
解题思路
给定一个由'1'(陆地)和'0'(水)组成的二维网格,需要计算其中岛屿的数量。岛屿的定义是被水包围的、通过水平或垂直方向相邻连接的陆地区域
所有连在一起的'1'算作一个岛屿,而单独的'1'或者被'0'分隔开的'1'群各自算作不同的岛屿
好的,我现在要解决“岛屿数量”这个问题。首先,我得弄清楚题目要求。题目是给定一个由'1'(陆地)和'0'(水)组成的二维网格,需要计算其中岛屿的数量。岛屿的定义是被水包围的、通过水平或垂直方向相邻连接的陆地区域。也就是说,所有连在一起的'1'算作一个岛屿,而单独的'1'或者被'0'分隔开的'1'群各自算作不同的岛屿。
首先,我需要想怎么遍历这个二维网格。常见的做法是使用深度优先搜索(DFS)或者广度优先搜索(BFS)。这两种方法都能遍历整个网格,当遇到一个'1'时,就将所有与之相连的'1'都标记为已访问,这样就不会重复计算同一个岛屿。
比如,上述图片中,共有三个岛屿:
- 左上角的四个'1'组成一个岛屿
- 中间的一个'1'是一个岛屿
- 右下角的两个'1'是第三个岛屿
使用深搜或广搜:当遇到一个'1'时,计数器加一,再将所有与之相连的'1'都标记为已访问,这样就不会重复计算同一个岛屿
方法思路
- 遍历网格:逐个检查每个格子
- 发现陆地:当遇到'1'时,表示发现一个新岛屿,计数器加 1
- 标记已访问:通过 DFS 将当前岛屿的所有相连陆地标记,当遇到已标记过的陆地节点和海洋节点直接跳过(避免重复计数)
- 递归边界:确保搜索时行和列不越界,且仅处理未被访问的陆地
需要初始化地图,然后使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历
代码
function numIslands(grid) {
if (!grid?.length) return 0
const rows = grid.length
const cols = grid[0].length
const directions = [
[0, 1],
[1, 0],
[0, -1],
[-1, 0],
]
const visited = new Array(rows).fill().map(() => new Array(cols).fill(false)) // 用于标记哪些节点已经访问过,避免重复访问
let isLandCount = 0
// 递归访问当前节点的所有相邻陆地节点
const dfs = (x, y) => {
// 每次递归调用时,标记当前节点为已访问
visited[x][y] = true
for (const [dx, dy] of directions) {
const nextX = dx + x
const nextY = dy + y
if (
nextX >= 0 &&
nextX < rows &&
nextY >= 0 &&
nextY < cols &&
!visited[nextX][nextY] &&
grid[nextX][nextY] === '1'
) {
dfs(nextX, nextY)
}
}
}
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (!visited[i][j] && grid[i][j] === '1') {
isLandCount++
dfs(i, j)
}
}
}
return isLandCount
}
ACM 格式
const r1 = require('readline').createInterface({ input: process.stdin })
// 创建readline接口
let iter = r1[Symbol.asyncIterator]()
// 创建异步迭代器
const readline = async () => (await iter.next()).value
let graph
let N, M
let visited
let result = 0
const dir = [
[0, 1],
[1, 0],
[0, -1],
[-1, 0],
]
// 读取输入,初始化地图
const initGraph = async () => {
let line = await readline()
;[N, M] = line.split(' ').map(Number)
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
for (let i = 0; i < N; i++) {
line = await readline()
line = line.split(' ').map(Number)
for (let j = 0; j < M; j++) {
graph[i][j] = line[j]
}
}
}
/**
* @description: 从节点x,y开始深度优先遍历
* @param {*} graph 是地图,也就是一个二维数组
* @param {*} visited 标记访问过的节点,不要重复访问
* @param {*} x 表示开始搜索节点的下标
* @param {*} y 表示开始搜索节点的下标
* @return {*}
*/
const dfs = (graph, visited, x, y) => {
for (let i = 0; i < 4; i++) {
const nextx = x + dir[i][0]
const nexty = y + dir[i][1]
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue
if (!visited[nextx][nexty] && graph[nextx][nexty] === 1) {
visited[nextx][nexty] = true
dfs(graph, visited, nextx, nexty)
}
}
}
;(async function () {
// 读取输入,初始化地图
await initGraph()
// 统计岛屿数
for (let i = 0; i < N; i++) {
for (let j = 0; j < M; j++) {
if (!visited[i][j] && graph[i][j] === 1) {
// 标记已访问
visited[i][j] = true
// 遇到没访问过的陆地,+1
result++
// 深度优先遍历,将相邻陆地标记为已访问
dfs(graph, visited, i, j)
}
}
}
console.log(result)
})()
99. 岛屿数量 广度优先搜索
将上述问题改为广搜,主要在于 bfs 函数的改动
广搜和深搜的核心目标是相同的:找到所有相连的陆地并标记为已访问
const bfs = (x, y) => {
const queue = []
queue.push([x, y])
visited[x][y] = true
while (queue.length > 0) {
const [curX, curY] = queue.shift()
for (const [dx, dy] of directions) {
const nextX = curX + dx
const nextY = curY + dy
if (
nextX >= 0 &&
nextX < rows &&
nextY >= 0 &&
nextY < cols &&
!visited[nextX][nextY] &&
grid[nextX][nextY] === '1'
) {
queue.push([nextX, nextY])
visited[nextX][nextY] = true
}
}
}
}
- bfs 函数用于从当前节点开始,广度优先搜索所有相邻的陆地节点
- 使用队列存储当前需要访问的节点
- 每次从队列中取出一个节点,检查其四个方向的邻接节点
- 如果邻接节点是未访问的陆地,将其加入队列并标记为已访问
bfs 和 dfs 代码区别
以示例为例
DFS:
- 从起始点出发,优先沿着一个方向深入搜索,直到无法继续,再回溯到上一个节点
- 搜索路径:(0,0) → (0,1) → (1,1) → (1,0)
BFS:
- 从起始点出发,按层次逐步扩展搜索范围
- 搜索路径:(0,0) → (0,1) → (1,0) → (1,1)
岛屿的最大面积
之前已经计算出岛屿数量,现在需要进一步找到其中最大的岛屿面积
可以在计算岛屿数量的基础上稍作调整,核心思路保持一致,主要新增面积统计功能
与岛屿数量的差异
新增面积统计:每次发现一个岛屿时,需计算其面积,并更新最大面积
逻辑调整
- 初始化当前岛屿面积 count = 0
- 每扩展一个相邻陆地节点,面积加 1
- 完成一个岛屿的遍历后,比较并更新全局最大值
其余部分(如网格遍历、队列操作、边界检查、标记已访问节点)与原问题完全一致
function maxAreaOfIsland(grid) {
if (!grid || grid.length === 0) return 0
const rows = grid.length
const cols = grid[0].length
const directions = [
[0, 1], // 右
[1, 0], // 下
[0, -1], // 左
[-1, 0], // 上
]
let maxArea = 0
// 深度优先搜索函数
const dfs = (x, y) => {
if (x < 0 || x >= rows || y < 0 || y >= cols || grid[x][y] === 0) {
return 0
}
grid[x][y] = 0 // 标记为已访问
let area = 1 // 当前节点的面积为 1
for (const [dx, dy] of directions) {
area += dfs(x + dx, y + dy) // 累加相邻陆地的面积
}
return area
}
// 遍历整个网格
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (grid[i][j] === 1) {
const area = dfs(i, j) // 计算当前岛屿的面积
maxArea = Math.max(maxArea, area) // 更新最大面积
}
}
}
return maxArea
}
京ICP备2022027737号
Copyright © 2022 - present @wangxiang