跟着卡哥学算法Day 13：二叉树 & 遍历

正在加载今日诗词....

2025-02-24

二叉树基础

树形结构，每个节点最多有两个子节点，称为左子节点和右子节点。

根节点：顶级节点，没有父节点
叶子结点：没有子节点的节点
子树：每个节点的左、右子节点分别构成左子树和右子树
深度：从根节点到最远叶子节点的最长路径上的节点数

分类

// 构建示例树:
//       1
//      / \
//     2   3
//    / \
//   4   5

普通二叉树

任意节点最多有两个子节点

满二叉树

所有叶子结点都在同一层
深度为 k 的满二叉树，最多有 2^k - 1 个节点

完全二叉树

除最后一层外，其他层节点必须填满，并且最后一层叶子节点必须靠左
若最底层为第 h 层（h 从 1 开始），则该层包含 1~ 2^(h-1) 个节点。

二叉搜索树 BST

左子树所有节点值 < 根节点值
右子树所有节点值 > 根节点值

平衡二叉搜索树 AVL

任意节点的左右子树高度差不超过 1
左右子树都会平衡二叉树

二叉树的存储方式

链式存储
顺序存储

一般使用链式存储

二叉树的遍历

深度优先遍历

先往深走，遇到叶子结点再往回走

前序遍历：中左右
中序遍历：左中右
后序遍历：左右中

如下图例子所示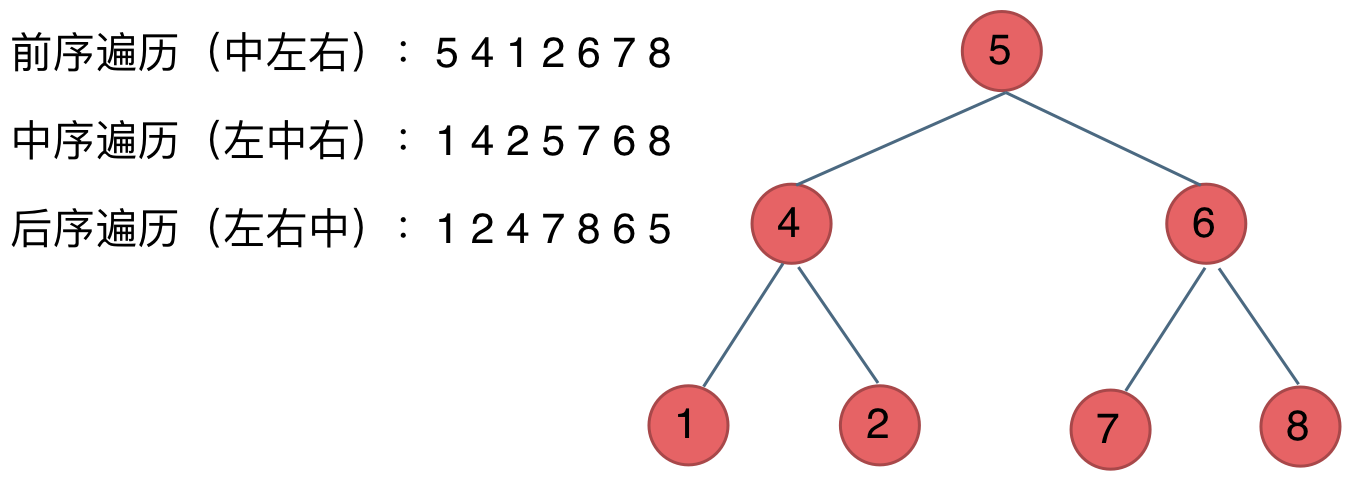： binary-tree-sort

这里的前中后，指的是中间节点的遍历顺序

广度优先遍历

一层一层遍历

二叉树的定义

// ES5
function TreeNode(val) {
  this.val = val // 节点值
  this.left = null // 左子节点（默认为空）
  this.right = null // 右子节点（默认为空）
}

// ES6
class TreeNode {
  constructor(val) {
    this.val = val
    this.left = null
    this.right = null
  }
}

二叉树递归排序

递归方法论：

确定递归的参数和返回值
确定终止条件，如果没有终止，会导致栈溢出
确定单层递归的逻辑

以前序遍历（根 -> 左 -> 右）为例：

确定递归的参数和返回值
- 递归参数：当前遍历节点
- 返回值：存储遍历节点的数组
确定终止条件
- 如果本层遍历节点为空，则直接 return
确定单层递归的逻辑
- 前序遍历：中左右

// 前序遍历
function preorderTraversal(root) {
  if (!root) return []
  return [
    root.val,
    ...perorderTraversal(root.left),
    ...preorderTraversal(root.right),
  ]
}

// 中序遍历
function inorderTraversal(root) {
  if (!root) return []
  return [
    ...perorderTraversal(root.left),
    root.val,
    ...preorderTraversal(root.right),
  ]
}

// 后序遍历
function postorderTraversal(root) {
  if (!root) return []
  return [
    ...perorderTraversal(root.left),
    ...preorderTraversal(root.right),
    root.val,
  ]
}

二叉树迭代遍历（非递归）

递归在底层也是通过栈来实现的

通过栈来模拟现二叉树的迭代遍历，避免递归造成的溢出风险

前序遍历

初始化栈，将根节点入栈
循环处理：
1. 弹出栈顶元素，数值保存到数组中
2. 如果有右子节点，入栈（先右后左，保证左子树先出栈）
3. 如果有左子节点，入栈
如果栈为空，则遍历结束

function preorderTraversal(root) {
  if (!root) return []
  const stack = [root]
  const result = []

  while (stack.length) {
    const current = stack.pop()
    result.push(current.val)

    if (current.right) stack.push(current.right)
    if (current.left) stack.push(current.left)
  }
  return result
}

中序遍历

遍历二叉树的迭代过程，主要有两个操作：

访问：遍历节点
处理：将元素放进 result 数组中

中序遍历和前序遍历不同的是：

前序遍历：先访问中间节点，同时处理的也是中间节点，即访问和处理的元素顺序一致
中序遍历：先访问根结点，然后一层一层向下访问，直到到达左子树的最底部，再进行处理

function inorderTraversal(root) {
  if (!root) return []
  const result = []
  const stack = []

  let cur = root
  while (cur || stack.length) {
    // 一直访问左子树，直到左子树为空
    while (cur) {
      stack.push(cur)
      cur = cur.left
    }

    // 循环处理栈
    cur = stack.pop()
    result.push(cur.val)
    // 处理右子树
    cur = cur.right
  }

  return result
}

后序遍历

前序遍历是中 -> 左 -> 右
后序遍历是左 -> 右 -> 中
只需要把前序遍历修改顺序成中 -> 右 -> 左的顺序，即先入栈左子树，再入栈右子树
再将数组结果进行反转（数指针）

function postorderTraversal(root) {
  if (!root) return []
  const result = []
  const stack = [root]

  while (stack.length) {
    const current = stack.pop()
    result.push(current.val)

    if (current.left) stack.push(current.left)
    if (current.right) stack.push(current.right)
  }

  return result.reverse()
}

二叉树的统一迭代法

上面写出的中序遍历与其他两个的迭代法风格不统一，其主要原因是：要访问和要处理的节点不一致。

此时可以将访问的节点放入栈中，再把要处理的节点也放入栈中但是需要另外做标记

如何标记

空指针标记法：要处理的节点放入栈后，紧接这放入一个空指针作为标记，当栈中弹出 null 时，表示下一个节点需要被处理（即加入结果）。

那么此时压栈顺序应该如下：

前序遍历：中 -> 左 -> 右，压栈顺序为：右 -> 左 -> 中 -> null
中序遍历：左 -> 中 -> 右，压栈顺序为：右 -> 中 -> null -> 左
后序遍历：左 -> 右 -> 中，压栈顺序为：中 -> null -> 右 -> 左

如：

// 构建示例树:
//       1
//      / \
//     2   3
//    / \
//   4   5

前序遍历：中 -> 左 -> 右，压栈顺序为：右 -> 左 -> 中 -> null

初始化栈，将 1 压入栈
循环处理：
1. 弹出栈顶元素
  1. 为 null，则下个元素就是要处理的元素，添加到结果中，继续处理下一个元素
  2. 不为 null，则继续处理当前元素
2. 压入 3，先右后左
3. 压入 2
4. 压入 null
返回结果

/**
 * 前序遍历统一迭代法
 * 顺序：中 -> 左 -> 右
 * 压栈顺序：右 -> 左 -> 中 -> null
 */
function preorderTraversal(root) {
  const result = []
  const stack = [root]
  while (stack.length) {
    const cur = stack.pop()

    if (!cur) {
      result.push(cur.pop().val)
      continue
    }

    if (cur.right) stack.push(cur.right)
    if (cur.left) stack.push(cur.left)
    stack.push(cur)
    stack.push(null)
  }
  return result
}

通过入栈顺序调整处理时机

入栈顺序决定了根节点的处理时机：

前序遍历：

stack.push(node)
stack.push(null) // 根节点标记为待处理
stack.push(node.right) // 右子节点入栈（后处理）
stack.push(node.left) // 左子节点入栈（先处理）

根节点先被处理（标记后立即弹出 null）。

中序遍历：

stack.push(node.right) // 右子节点入栈（后处理）
stack.push(node)
stack.push(null) // 根节点标记为待处理
stack.push(node.left) // 左子节点入栈（先处理）

根节点在左子树处理后处理。

后序遍历：

stack.push(node)
stack.push(null) // 根节点标记为待处理
stack.push(node.right) // 右子节点入栈（后处理）
stack.push(node.left) // 左子节点入栈（先处理）

根节点在左右子树均处理后处理。

统一迭代法的核心逻辑

通过 空指针标记 和 入栈顺序控制，将三种遍历统一为同一框架：

标记待处理的根节点：将根节点与空指针一起入栈(在统一迭代法中，无论是哪种遍历方式，处理节点的时机都是在中节点的位置)，表示该节点需要后续处理。
控制子节点的入栈顺序：调整左右子节点的入栈顺序，间接决定根节点的处理时机。

二叉树的层序遍历

深度优先遍历：递归和迭代都使用栈来实现
广度优先遍历：二叉树的层序遍历（一层一层遍历二叉树），需要借助队列来实现

思路

初始化队列：将根节点加入队列
循环处理队列：
1. 记录当前层的节点数量（队列长度）
2. 依次取出当前层的所有节点，并将它们的值存入当前层的结果列表
3. 将每个节点的非空左、右子节点加入队列
逐层收集结果：将每层的节点值列表合并为最终结果

//       1
//     /   \
//    2     3
//   / \     \
//  4   5     6

层序遍历过程：

初始队列：[1] → 处理第 1 层 → result = [[1]]，子节点入队 [2, 3]
处理第 2 层：弹出 2 和 3 → result = [[1], [2, 3]]，子节点入队 [4, 5, 6]
处理第 3 层：弹出 4、5、6 → result = [[1], [2, 3], [4, 5, 6]]

代码实现

function levelOrder(root) {
  if (!root) return []
  const result = []
  const queue = [root]

  while (queue.length) {
    const size = queue.length
    const curLevel = []

    for (let i = 0; i < size; i++) {
      const cur = queue.shift()
      curLevel.push(cur.val)

      if (cur.left) queue.push(cur.left)
      if (cur.right) queue.push(cur.right)
    }

    result.push(curLevel)
  }
  return result
}

leetcode 相关题目：

102.二叉树的层序遍历
107.二叉树的层次遍历 II 二叉树层序遍历后结果反转
199.二叉树的右视图二叉树层序遍历后遍历结果，拿子数组最后一个
637.二叉树的层平均值二叉树层序遍历不记录节点值，记录每层总和的平均值
429.N 叉树的层序遍历二叉树层序遍历往队列 push 下层节点时，不再是 left 和 right，而是遍历 children
515.在每个树行中找最大值二叉树层序遍历不记录节点值，记录每层最大值
116.填充每个节点的下一个右侧节点指针二叉树层序遍历如果不是每层最后一个节点，则将它的 next 指针指向队首，返回二叉树头节点
117.填充每个节点的下一个右侧节点指针 II 和 116 代码一摸一样
104.二叉树的最大深度二叉树层序遍历，记录一下遍历的层数就是二叉树的深度
111.二叉树的最小深度与 104 相似，只是当当前节点左右节点都为 null 时，提前返回 depth 深度

# 二叉树基础

# 分类

# 普通二叉树

# 满二叉树

# 完全二叉树

# 二叉搜索树 BST

# 平衡二叉搜索树 AVL

# 二叉树的存储方式

# 二叉树的遍历

# 深度优先遍历

# 广度优先遍历

# 二叉树的定义

# 二叉树递归排序

# 二叉树迭代遍历（非递归）

# 前序遍历

# 中序遍历

# 后序遍历

# 二叉树的统一迭代法

# 如何标记

# 通过入栈顺序调整处理时机

# 统一迭代法的核心逻辑

# 二叉树的层序遍历

# 思路

# 代码实现